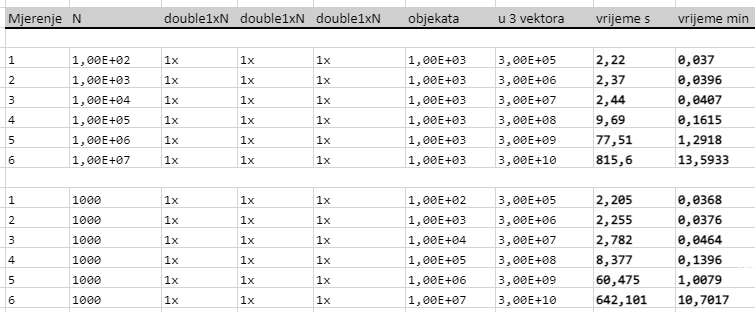
Analytic frequency response function
- A Frequency Response Function (FRF) is a function used to quantify the response
of a system to an excitation, normalized by the magnitude of this excitation, in the frequency domain
- This class fills three vectors< double > within itself
- frf values
- frequencies in Hz
- normalized freqencies 0,1,2 Nth value x f0, hint: zeta = 1/2Q ( here an "unsual" delta?)

- Purpose 1: I want to see how fast can I create millions of such computational objects, and how fast can c++ process it overally on my laptop
- Purpose 2: I want to reuse it in later project in QT framework
- So here the specs and definition of a class, then the measruement:
- Intel(R) Core(TM) i5-5300U CPU @ 2.30GHz 2.30 GHz
- 8,00 GB (7,88 GB available)
- 64-Bit, x64-basierter processor
sdof_analytic.h
Creating frf/transmisibility function
#include < iostream >
#include < string >
#include < sstream >
#include < cmath >
#include < iomanip >
#include < fstream >
#include < vector >
using namespace std;
class SDOF_SYS
{
// SDOF system parametric inputs
double f_min; // minimal frequency
double f_max; // maximal frequency
double fr; // resonant frequency
double Q; // Q - factor
int N; // number of points
// self calulated
double D; // damping
double freqR; // frequency resolution
double NOct; // number of octaves
public:
vector<double> sdof_frf; // vecotr of type double for frequency response function
vector<double> vec_f; // corresponding vector of frequencies in [Hz] <1x N>
vector<double> vec_r; // dimensionless frequencies from 0,1 .. in given N points <1x N>
// contructor
~SDOF_SYS(); // destructor
SDOF_SYS(); // empty constructor
SDOF_SYS(double, double, double, double, int); // full constructor
void showInfo();
vector FRF_fun();
};
// CONSTRUCTOR FUNCTIONS
SDOF_SYS::~SDOF_SYS(){
//cout << " \n memory clear \n";
}
SDOF_SYS::SDOF_SYS()
{
// some default system
// f_min = 10 Hz
// f_max = 1000 Hz;
// Resonator = 440Hz;
// Q = 120
// N = 100;
f_min = 10;
f_max = 1000;
fr = 440;
Q = 120;
N = 100;
D = 1/(2*Q);
freqR = (f_max - f_min) / N;
NOct = log2(f_max/f_min);
}
// overloading contructor with non defaults ..
SDOF_SYS::SDOF_SYS(double minf, double maxf, double RES, double Q_fact, int n){
f_min = minf;
f_max = maxf;
fr = RES;
Q = Q_fact;
N = n;
D = 1/(2*Q);
freqR = (f_max - f_min) / N;
NOct = log2(f_max/f_min) ;
}
// CLASS MEMBER FUNCTIONS
// show dynamical sdof ... system information
void SDOF_SYS::showInfo(){
cout << endl;
cout << "SDOF- FRF" << endl;
cout << " Starting frequency : "<< f_min << " [Hz] " << endl;
cout << " End frequency : "<< f_max << " [Hz] " << endl;
cout << " Frequency span : "<< f_max-f_min << " [Hz] " << endl;
cout << " Resonant frequency : "<< fr << " [Hz] " << endl;
cout << " Q- factor : "<< Q << " [v/v]" << endl;
cout << " Damping : "<< 100*D << " [ %]"<< endl;
cout << " Number of points : "<< N << " [-] " << endl;
cout << " Freq. resolution : "<< (f_max-f_min)/N << " [Hz] " << endl;
cout << " Number of octaves : "<< log2(f_max/f_min) << " [oct]" << endl;
}
//compte FRF function and return vectors
vector SDOF_SYS :: FRF_fun(){
vector y_frf; // sdof_frf vector
vector x_r; // r .dimensionless freq vector X - axis
vector x_df; // frequency field vector X - axis
// LOOP variables
double f; // frequency variable changing inside the loop
double df = (f_max - f_min)/N;
double r; // filed dimensionless
for (int i = 0; i < N+1; i++)
{
if(i==0)
f = f_min;
else
f += df;
// frequency filed that containtes
// f + df, fo + 2df + .... f_max .. i.e (f+df)/fr .. (f+2df)/r
r = f/fr;
x_df.push_back(f); //frequency vector
x_r.push_back(r); // frequecy vector <0, ..... 1 >
y_frf.push_back(1/(r*r)); // FRF vectro calculation
/*
cout << setw(7) << left << i << ". "
<< setw(10) << setprecision(4) << left << f
<< setw(10) << setprecision(3) << left << r
<< setw(10) << setprecision(3) << left << 1/(r*r) << endl;
*/
}
sdof_frf = y_frf;
vec_f = x_df;
vec_r = x_r;
return y_frf;
}
// aux function for printing out vector inside the SDOF_FRF
void read_vector(vector x)
{
vector::iterator pos;
for(pos = x.begin(); pos != x.end(); pos++ )
{
cout << setprecision(3)<< *pos<< " ";
}
}
main.cpp
main function
#include<iostream>
#include<fstream >
#include "sdof_analytic.h"
using namespace std;
int main()
{
Sdof_analytic sdofx(10, 2000, 660, 120, 1000);
cout << sdofx.sdof_info();
// compute the FRF functinos inside the sdof system
sdofx.FRF_THIS();
// PRINT SETUP ::: filenames...
string fileName = "sdof_data3.dat";
system_write(sdofx, fileName);
vector < double > k = sdofx.getFRFVector();
for (size_t i = 0; i < k.size(); i++)
{
cout << i << " " << k[i] << endl;
}
return 0;
}
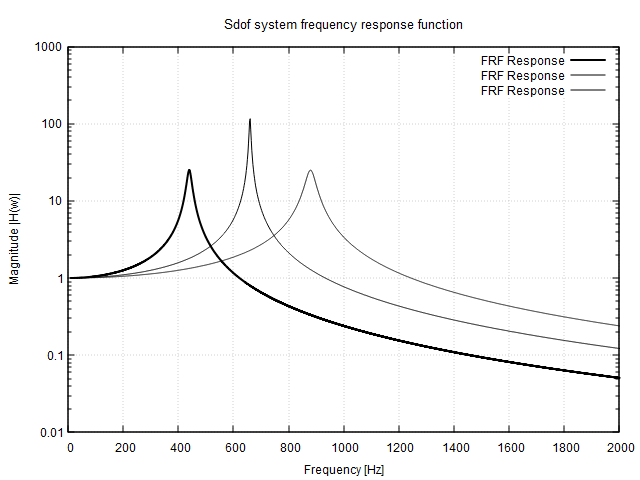
GnuPlot
When several FRFs plotted they should produce results as shown here..
set title "Sdof system frequency response function" font ",10"
set xlabel 'Frequency [Hz]'
set ylabel 'Magnitude |H(w)|'
set logscale y
set grid
plot 'sdof_data.dat' using 1:3 with line lt -1 lw 2 title 'FRF Response',\
'sdof_data1.dat' using 1:3 with line lt -1 lw 1 title 'FRF Response',\
'sdof_data3.dat' using 1:3 with line lt -1 lw 1 title 'FRF Response',\
speed test with this object and c++
This is a single resonator object example
SDOF- FRF
Starting frequency : 10 [Hz]
End frequency : 500 [Hz]
Frequency span : 490 [Hz]
Resonant frequency : 440 [Hz]
Q- factor : 120 [v/v]
Damping : 0.416667 [ %]
Number of points : 20 [-]
Freq. resolution : 24.5 [Hz]
Number of octaves : 5.64386 [oct]
vector1; [ 1x N ]
vector2; [ 1x N ]
vector3; [ 1x N ]
SYSTEM MODE ::: [ freq / r / FRF] ... :
vector1 ::: frequencies
10 34.5 59 83.5 108 132 157 182 206 230 255 280 304 328 353 378 402 426 451 476 500
vector2 ::: dimensionless frequencies (1 at the resonance)
0.0227 0.0784 0.134 0.19 0.245 0.301 0.357 0.412 0.468 0.524 0.58 0.635 0.691 0.747 0.802 0.858 0.914 0.969 1.02 1.08 1.14
vecotr3 ::: calculated FRF function
1.94e+03 163 55.6 27.8 16.6 11 7.85 5.88 4.56 3.64 2.98 2.48 2.09 1.79 1.55 1.36 1.2 1.06 0.952 0.856 0.774
- This is a laptop speed test where I've changed numer of points within the loop and did some time measurements.
Here is how c++ performs on my pc.
- a) First I am extending the vectors within the objects I am calling "resonators"
- b) Then I am extending the number of objects, but i am keeping the vectors constant
.......................................................................................................................
TEST 1
Increasing frequency resolution from 100 points to 10 milion points in each vector
......................................................................................................................
1000 resonators with 100 points in three vectors returned to itself
[Done] exited with code=0 in 2.222 seconds
1000 resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 2.374 seconds
1000 resonators with 10000 points in three vectors returned to itself
[Done] exited with code=0 in 2.443 seconds
1000 resonators with 100,000 points in three vectors returned to itself
[Done] exited with code=0 in 9.691 seconds
1000 resonators with 1,000,000 points in three vectors returned to itself
[Done] exited with code=0 in 77.508 seconds
1000 resonators with 10,000,000 points in three vectors returned to itself
[Done] exited with code=0 in 815.599 seconds
.............................................
100 Resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 2.205 seconds
1000 Resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 2.255 seconds
10000 Resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 2.782 seconds
100.000 Resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 8.377 seconds
1.000.000 Resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 60.475 seconds
10.000.000 Resonators with 1000 points in three vectors returned to itself
[Done] exited with code=0 in 642.101 second
Strange, it is better to have larger number of objects and keep the vectros shorter, but only after 1e6 points in total