"sdof_digital.h"
Explanation *ISO 18431-4 Standard
#ifndef SDOF_DIGITAL_H
#define SDOF_DIGITAL_H
#include &l tiostream >
#include &l cmath >
#include &l string >
#include &l sstream >
//using namespace std;
/* DIGITAL H(w) = FRF(f) ===== > to H(z)
_____ _____ ____ ______ * . Q = 1/2D
/ ____| __ \ / __ \| ____| | / \
| (___ | | | | | | | |__ |..../ | \
\___ \| | | | | | | __| | fr \............... [N]
____) | |__| | |__| | | |------------------------->
|_____/|_____/ \____/|_| | |
fmin fmax
DIGITAL SYSTEM ::: sdof_digital.h
// Difference equation for computation of extreme response spectrum
// Explanation *ISO 18431-4 Standard
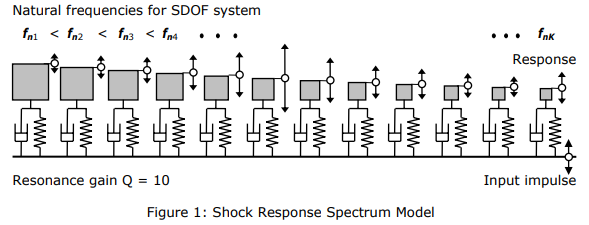
Response of a linear Single Degree of Freedom System (SDOF system) to vibration,
according to its natural frequency, for a given damping ratio. The response is
described here by the relative movement of the mass of this system in relation
to its support.
//x2 = β0 x1 k + β1 x1(k −1)+ β2 x1(k − 2) − α1x2(k −1) − α2 x2(k − 2)
// RECALCULATING SDOF filter coefficients
/* Shock
Response Spectrum is defined as the response to a given acceleration
acting at a set of mass-damper-spring oscillators
wnS / Q + wn^2
A2/A1 = ______________________ --> transformed to Z domain ....
s^2 + (wn/Q)S +1
b0 + b1*z^-1 + b2*z^-2
H(z) = _________________________
1 + a1*z^-1 + a2*z^-2
Jan Gusic, 7.5, 2021
*/
/* DIGITAL SYSTEM FORM ***************************************************************
Sdof_digital is a calss for calculating coefficients, which are in turn returned to the
member structure C ( coefficients) ... this structure holds the difference equation coeffs.
C --- | a1
| a2
| b0
| b1
| b2
Now returning the structure to the public structure of 'deq' ( diff. equations interface)
coefficients are taken by the internal function
deq MyEquation;
Sdof_digital SDOF; which returns structure C after calling returnCoefficients()
( Ex. for first coefficients can be called SDOF.returnCoefficients().a1, .. )
Now, put the SDOF to Diff equation for single value as...
MyEquation.process(Sdof_digital::C& Coeff, 0 )
And check the coefficients passed by reference from Sdof_digital instance as
MyEquation.type()
cout << SDOF.type();
//they should be the same..
FOR EACH signal value in signal_in
MyEquation.process(SDOF.returnCoefficients(), signal_in(i))
END
*/
class Sdof_digital
{
private:
double PI = 3.14159265358979323846; //| pi
double fs; //| sampling f
double fr; //| resonance
double Q; //| Q
double Ts; //| samp. time
double wn; //| nat, freq.
// BiQuad filter coefficients
double A, B;
double b0,b1,b2;
double a1, a2;
public:
struct C{
double b0,b1,b2, a1, a2;
};
Sdof_digital(/* default == Bypass */); //| Bypass sinal
Sdof_digital(double, double, double); //| Digital system initialization
~Sdof_digital();
std::string type(); //| write coefficients to the screen
C returnCoefficients(); //| function returns C structure after reading them ..
};
Sdof_digital::Sdof_digital()
{ //bypass coefficients for xin = xout .. no processing
// with this fitler * off
b0 = 1;
b1 = b2 = 0;
a1 = a2 = 0;
}
std::string Sdof_digital::type()
{
std::stringstream sout;
sout << "| fs:" << this->fs << "| fr:" << fr << "| Q: " << Q << "\n";
sout << "| a0:" << this->a1 << " | a1:" << this->a2 << "\n";
sout << "| b0:" << this->b0 << "| b1:" << this->b1 << "| b2:"<< this->b2 <<"\n";
return sout.str();
}
Sdof_digital::~Sdof_digital()
{
}
Sdof_digital::Sdof_digital(double Fs, double fr, double Q)
{ //| sampling
//| | frequency
//| | Q
this->fs = Fs;
this->Ts = 1/fs;
this->wn = 2*PI*fr;
this->fr = fr;
this->Q = Q;
this->A = wn*Ts/2/Q;
this->B = wn*Ts*sqrt(1-1/4/Q/Q);
this->b0 = 1-exp(-A)*sin(B)/B;
this->b1 = 2*exp(-A)*(sin(B)/B-cos(B));
this->b2 = exp((-2)*A)-exp(-A)*sin(B)/B;
this->a1 = (-2)*exp((-1)*A)*cos(B);
this->a2 = exp((-2)*A);
}
Sdof_digital::C Sdof_digital::returnCoefficients()
{
C coeff;
coeff.b0 = this->b0;
coeff.b1 = this->b1;
coeff.b2 = this->b2;
coeff.a1 = this->a1;
coeff.a2 = this->a2;
return coeff;
}
// Difference equation
struct deq
{
// coefficients
double b0, b1, b2;
double a1,a2;
//input history
double x1,x2;
//output history
double y1, y2;
// procesurianje ::: Biquad filter normalized
double process(const Sdof_digital::C& COEFF,double x0){
b0 = COEFF.b0;
b1 = COEFF.b1;
b2 = COEFF.b2;
a1 = COEFF.a1;
a2 = COEFF.a2;
double y0 = b0*x0 + b1*x1 + b2*x2 - a1*y1 -a2*y2;
x2 = x1;
x1 = x0;
y2 = y1;
y1 = y0;
return y0;
}
// type the filtering coefficients to the console ..
void type()
{
std::cout << "\n\n Difference equation setup:::";
std::cout <<"| bo:" << b0 << "| b1: " << b1 << "|b2: " << b2 << std::endl;
std::cout <<"| a1:" << a1 << "| a2:" << a2 << "... " << std::endl;
}
};
#endif
main.cpp
#include "sdof_digital.h"
#include "signal_gen.h"
using namespace std;
// Functionality of sdof_digital.h
// herewith confrimed ..
//
//
int main()
{
//(1)
// Define Digital system :: Sdof_digital MySdof(fs,fr,Q)
Sdof_digital sys1;
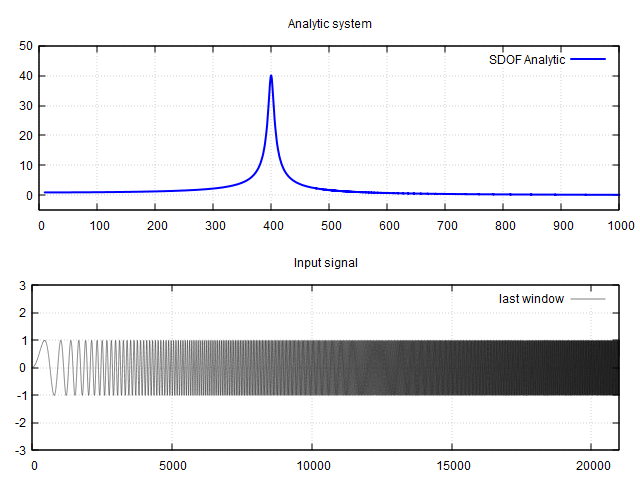
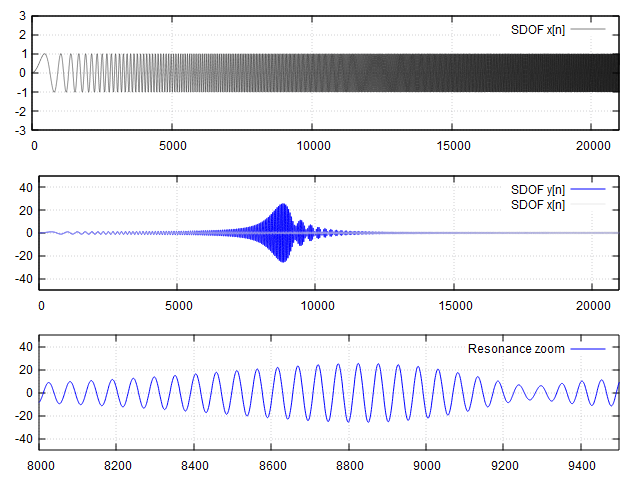
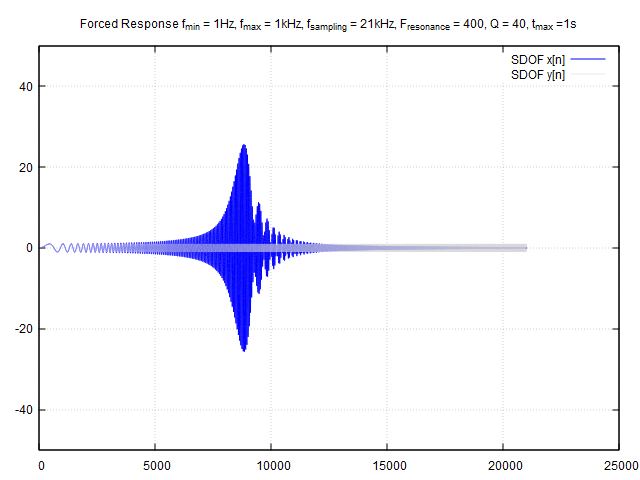
Sdof_digital sys2(21000, 400, 40);
cout << sys2.type();
//(2)
// Define Digital process :: deq CH_X; i.e. Turn the system to H(z) , get coefficients
// then CH_X(const Sdof_digital::C&, signal_input )
deq CH1;
CH1.process(sys2.returnCoefficients(),1);
CH1.type();
//(3)
// Define input signal from signal_gen.h
signal_gen sineWave;
sineWave.sweep_linear(21000,1, 1e3, 1, 0,1);
vector <double> x = sineWave.getSignal();
//(4)
// define the output vector to receive processed series ...
vector < double > y; double yy;
//(5)
// process the series
// x2 = β0 x1 k + β1 x1(k −1)+ β2 x1(k − 2) − α1x2(k −1) − α2 x2(k − 2)
for (size_t i = 0; i < x.size(); i++)
{
yy = CH1.process(sys2.returnCoefficients(), x[i]);
y.push_back(yy);
}
//(6) write to file for Gnuplot..
ofstream results("mySys_test.dat");
for(size_t i = 0; i < y.size(); i++){
results << i << "\t" << x[i] << "\t" << y[i] <<endl; }
results.close(); return 0;
}